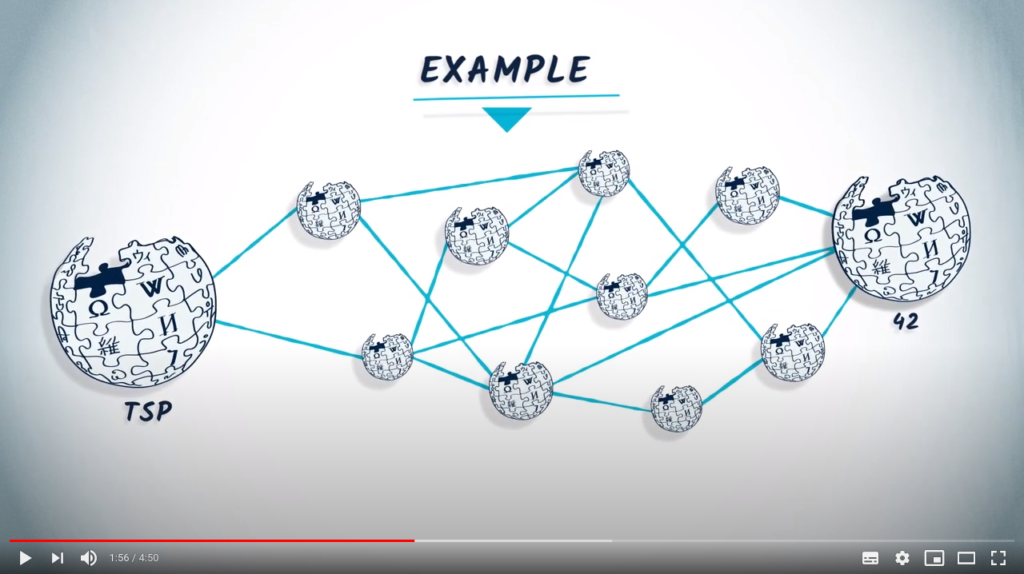
Heuristics and optimal solutions
As stated before, the use of heuristics may lead to finding a correct solution to a problem, but not necessarily the optimal one. This is the case for instance of the greedy approach, that iteratively choses locally optimal solutions to estimate a global optimum.
Still, using a heuristic does not always make a solution non-optimal. Recall for instance the bruteforce algorithm with backtracking studied previously.
The efficiency of backtracking strongly depends on the order in which branches of the tree of solutions are explored. In Lab 5, you probably have chosen to visit remaining vertices in the meta-graph as they come in your meta-graph structure like this:
def tsp (meta_graph, initial_vertex) :
...
for neighbor in meta_graph[vertex] :
if neighbor not in explored_vertices :
# Explore that branch
...
However, using a heuristic to encode an intuition on which neighbor should be explored first may be a good idea, as — if it is a good heuristic — it could lead to exploration of short paths quickly, thus leading to pruning numerous branches.
The following pseudo-code is a possible solution, in which we propose to use a min-heap, that will contain all neighbors, with an associated value corresponding to the score given by the heuristic. Since it is a min-heap, the lower the score, the better the quality of the neighbor:
def heuristic (neighbor, ...) :
# Return some score for the neighbor to evaluate
def evaluate_neighbors (neighbors, ...) :
scores = create_structure()
for neighbor in neighbors :
score = heuristic(neighbor, ...)
push_to_structure(scores, (score, neighbor))
return scores
def tsp (meta_graph, initial_vertex) :
...
non_visited_neighbors = [neighbor for neighbor in meta_graph[vertex] if neighbor not in explored_vertices]
scores = evaluate_neighbors(non_visited_neighbors, ...)
while len(scores) > 0 :
best_score, best_neighbor = pop_from_structure(scores)
# Explore that branch
...
You can for instance try to choose as a heuristic to return a score which is the distance between the vertex being explored and the candidate neighbor, i.e., the weight in the meta-graph.
Meta-heuristics
The meta prefix indicates that the word it is associated with is set to a higher level of abstraction. In this case, a meta-heuristic is a heuristic that will itself be used to find heuristics to solve a problem.
Meta-heuristics makes it possible to abstract the problem of finding the right heuristics, by considering heuristics as a solution to an optimization problem, whose objective is to maximize precision on the problem studied, while limiting complexity. Thus, a meta-heuristic is an algorithm that will go through the space of possible heuristics, and choose one that will be judged more optimal than the others according to certain criteria (hence the heuristic part in the word).
Meta-heuristics completely ignore the problem studied, considering that the heuristics sought is just a function that must be optimized to minimize a criterion. Thus, the same meta-heuristic can be used to produce heuristics that respond to a very large number of problems.
Some of the most well-known meta-heuristics are ant colonies, genetic algorithms, simulated annealing, etc.