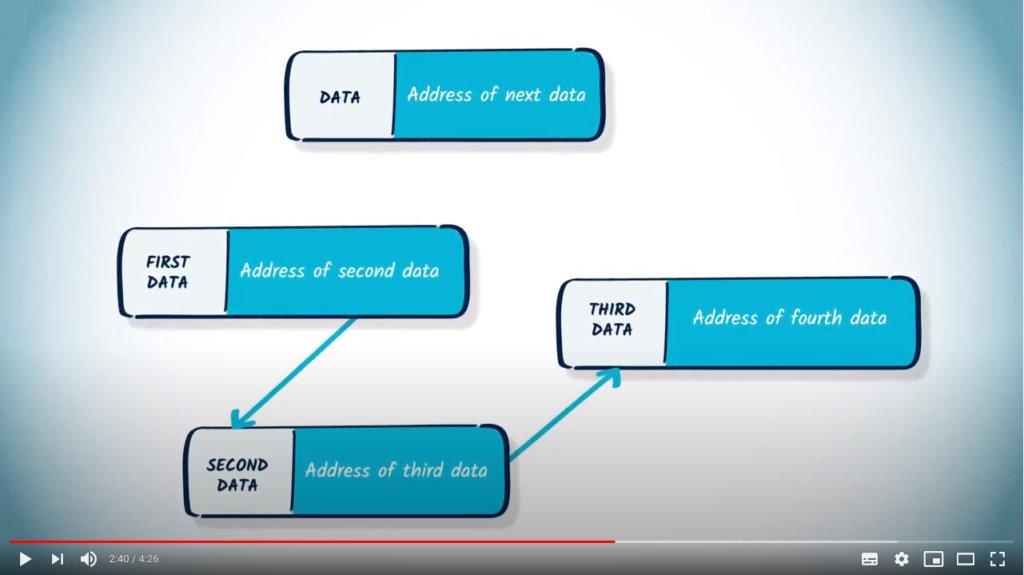
More details on the list-based solution
We have seen before that an adjacency matrix is a convenient object for representing a graph in memory.
However, in most cases, graphs are sparse objects, i.e., the number of existing edges is low compared to the number of edges of a complete graph. A direct implication is that most of the entries of the adjacency matrix are 0s. Since the number of elements in an adjacency matrix is equal to the square of the graph order, this can quickly lead to a lot of memory space used.
A possible solution to circumvent this problem is to use a different data structure: a list of lists. Let us call such an object ![]() , with
, with ![]() being lists. In this structure,
being lists. In this structure, ![]() (
(![]() ) will represent the edges that can be accessed from vertex
) will represent the edges that can be accessed from vertex ![]() .
.
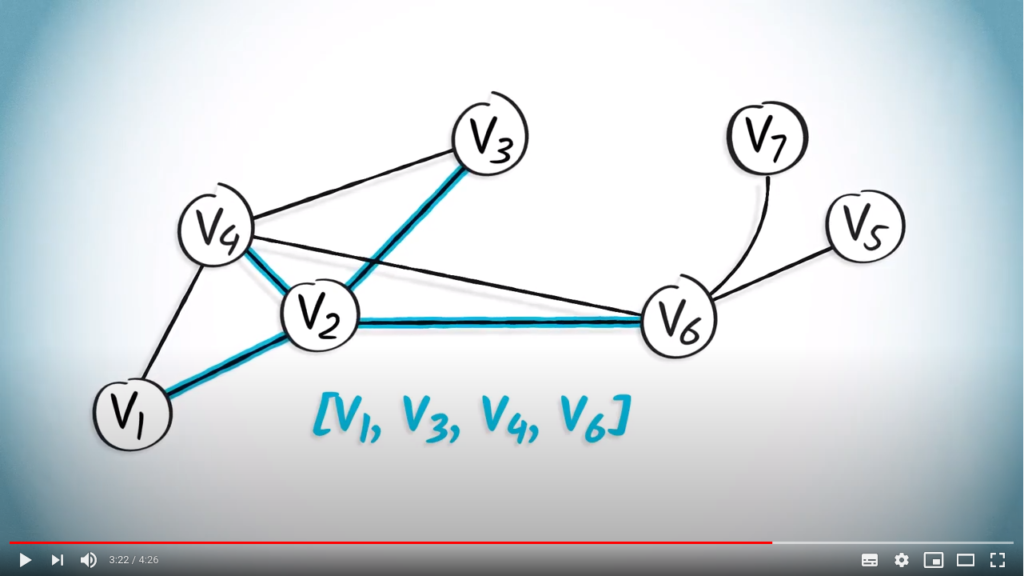
As an example, consider the following adjacency matrix:  .
.
Assuming vertices to be labelled from 1 to ![]() , this matrix is equivalent to the list
, this matrix is equivalent to the list ![]() .
.
We can quickly notice that the number of stored numbers has shrunk from ![]() to
to ![]() .
.
While this solution saves some memory space, it suffers from different limitations:
- Checking existence of an edge
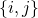 requires to go through all elements of the list
requires to go through all elements of the list 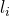 to verify if
to verify if 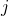 is one of its elements. This can take some time if
is one of its elements. This can take some time if 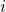 has a lot of neighbors. In comparison, making the same check with an adjacency matrix
has a lot of neighbors. In comparison, making the same check with an adjacency matrix 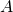 takes a single operation, as one just need to verify that
takes a single operation, as one just need to verify that ![Rendered by QuickLaTeX.com A[i, j] \neq 0](https://formations.imt-atlantique.fr/pyrat/wp-content/ql-cache/quicklatex.com-2a964de50305823f1ab199449c8d3aee_l3.png) .
. - It is not as easy to extend to weighted graphs. In the case of adjacency matrices, entries represent the weight associated with the edge. Here, entries are indices of non-zero elements, which cannot be altered without creating/deleting edges. A possible solution is to replace the lists of indices
![Rendered by QuickLaTeX.com l_i = [j, k, \dots]](https://formations.imt-atlantique.fr/pyrat/wp-content/ql-cache/quicklatex.com-7ebcdc223b25f76257bee19182ba6d5a_l3.png) with lists of couples
with lists of couples ![Rendered by QuickLaTeX.com l_i = [(j, w_j), (k, w_k), \dots]](https://formations.imt-atlantique.fr/pyrat/wp-content/ql-cache/quicklatex.com-1d67aa93304962d658c3d2806078360d_l3.png) , where
, where 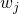 is the weight of edge
is the weight of edge 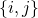 .
.
To go further
- Understanding the efficiency of GPU algorithms for matrix-matrix multiplication: A research paper illustrating one of the main reasons why matrices are frequently used.
- Graph Processing on FPGAs: Taxonomy, Survey, Challenges: A research paper illustrating the use of specific hardware (here, FPGA) for processing large graphs.



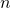 -th piece of data of an array. On the other hand, accessing the
-th piece of data of an array. On the other hand, accessing the 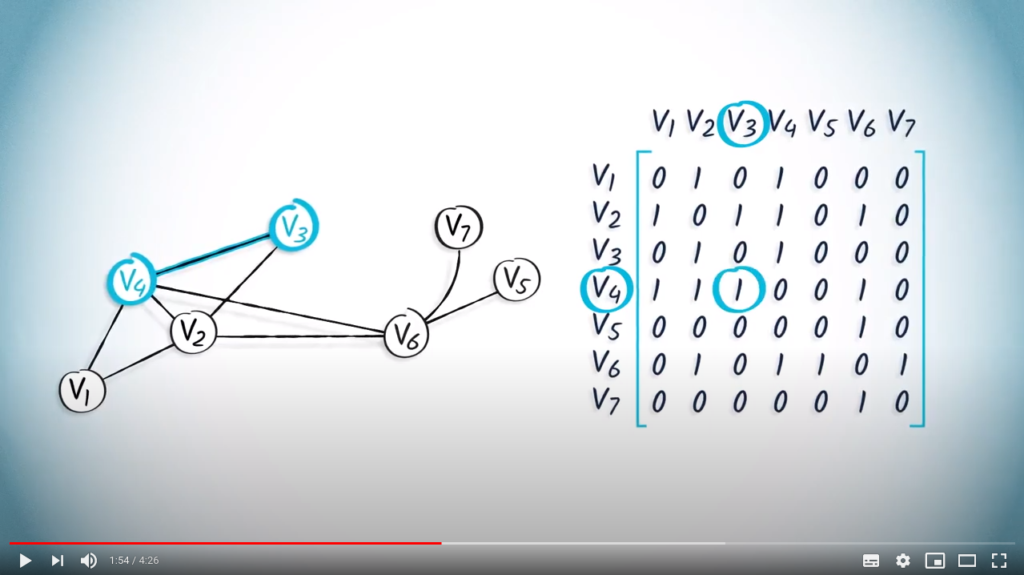
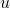 and
and  are connected by an edge.
are connected by an edge.