Hi everyone! In today’s lesson, we will see how to build routing tables to navigate a graph, using the spanning trees obtained from graph traversal algorithms, such as the BFS or the DFS.
These routing tables will help the artificial intelligence that you will develop in this course to move between two positions in the maze.
From spanning trees to routing
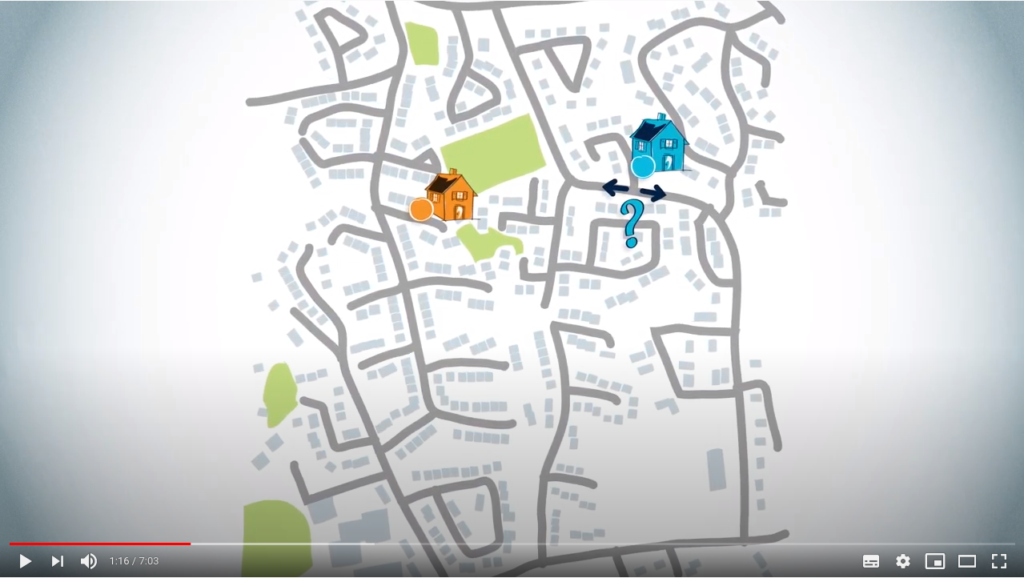
Routing from a starting point to a destination is interpreted backwards. We already know what the starting point is, so we need to begin with the destination to find a path. So, a routing algorithm provides a path from the destination to the starting point.
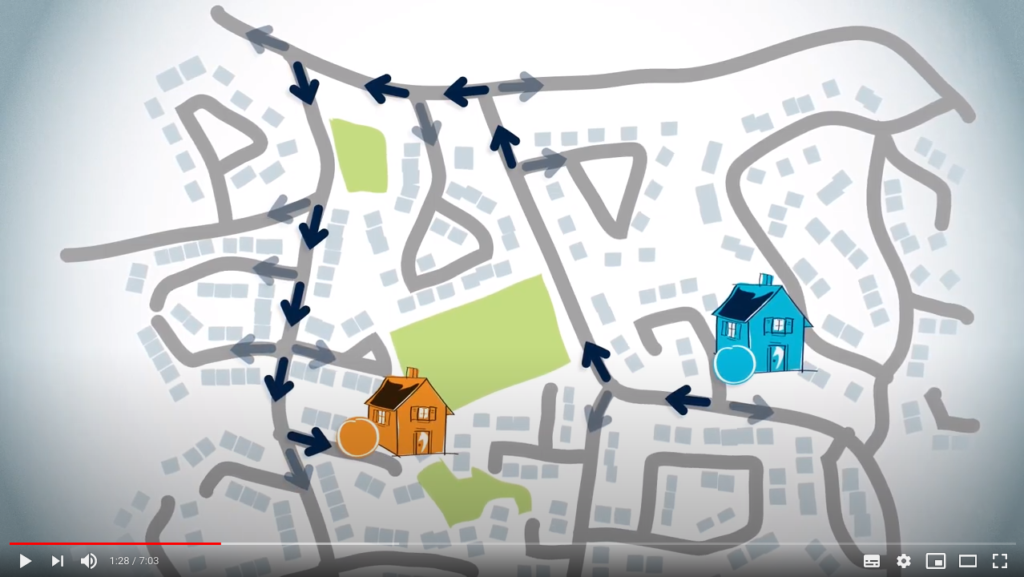
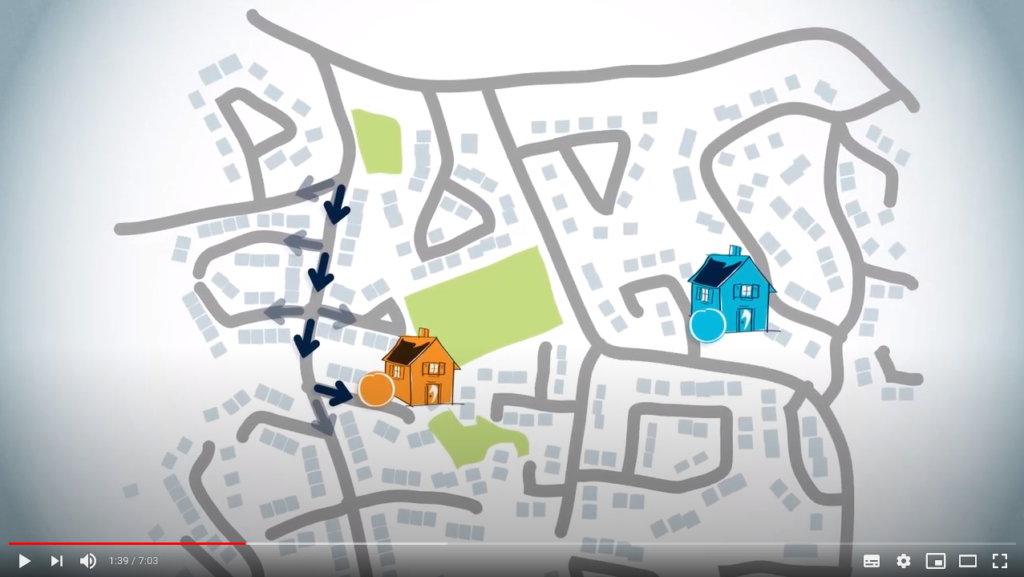
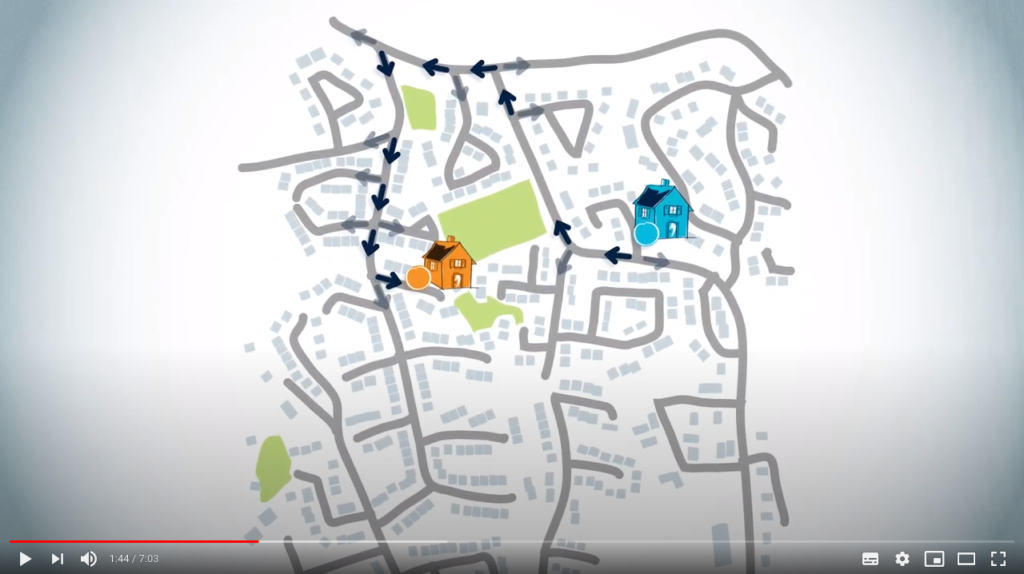
This second way of thinking is how the routing algorithm will work.

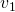 and
and 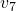 .
.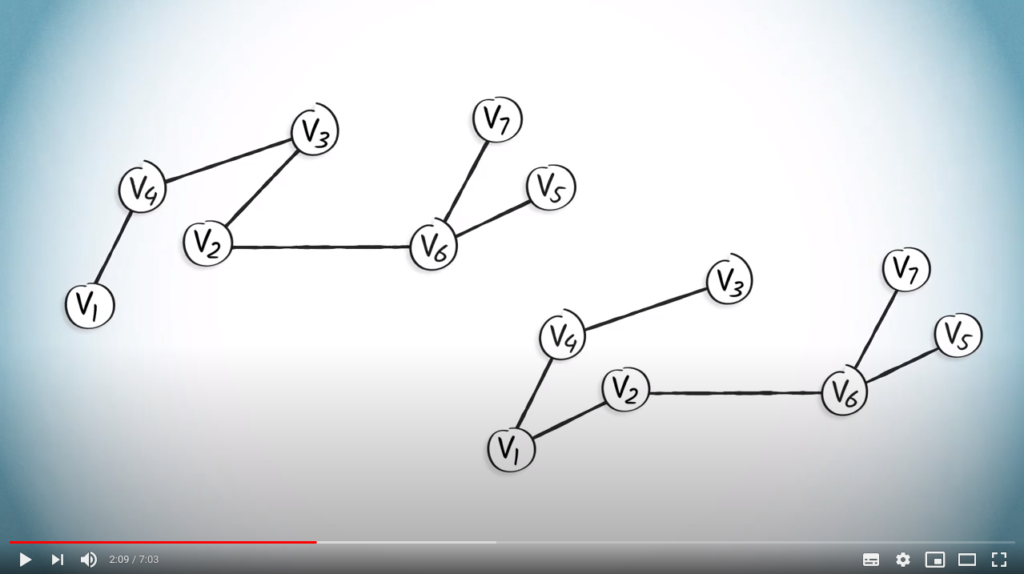
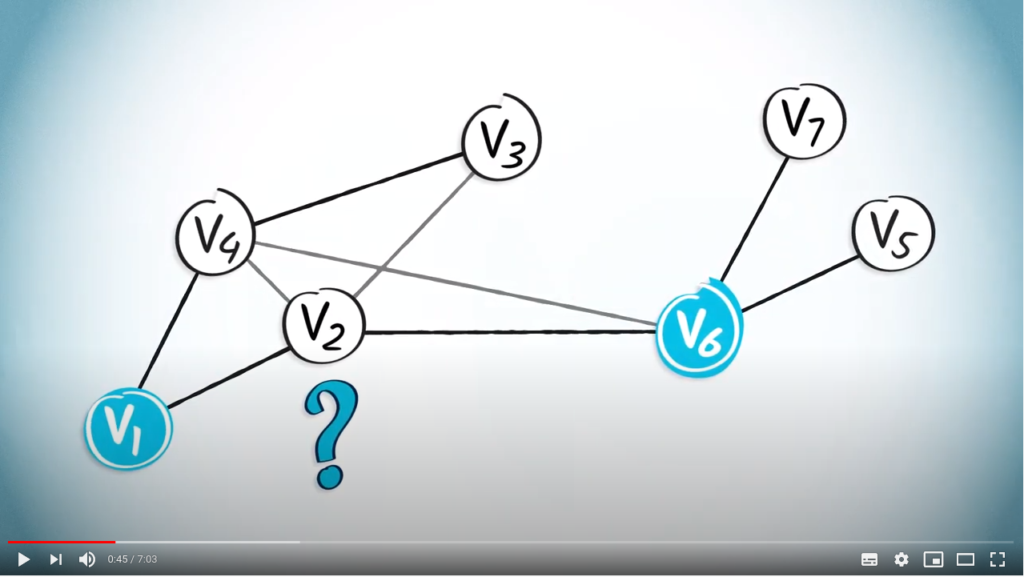
Routing from ![]() to any other vertex can be easy when we use trees. But to do this, we first need a few more definitions.
to any other vertex can be easy when we use trees. But to do this, we first need a few more definitions.
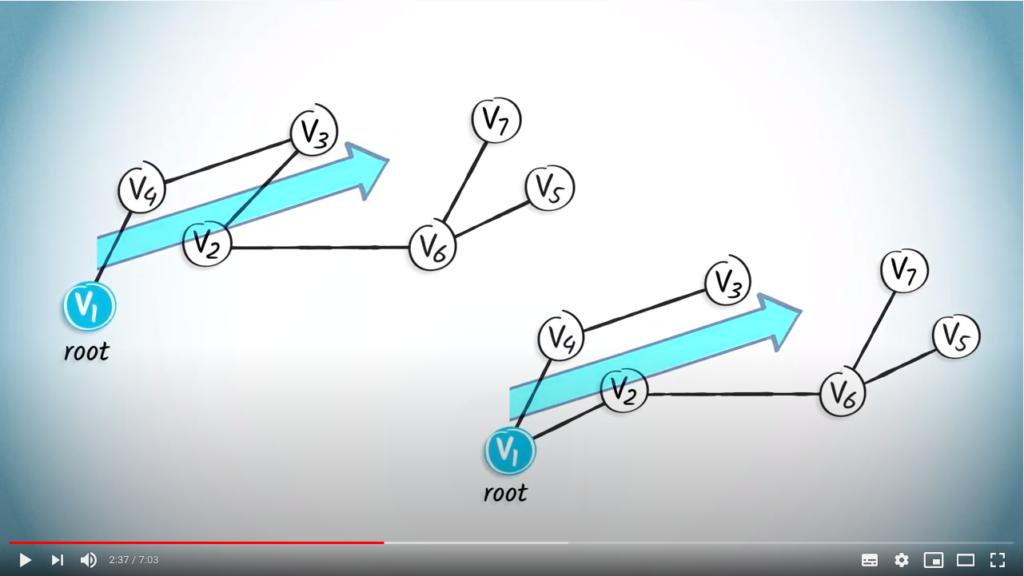
 as the root, because it’s our starting position. Therefore, the edges of this rooted tree have a natural orientation away from the root.
as the root, because it’s our starting position. Therefore, the edges of this rooted tree have a natural orientation away from the root.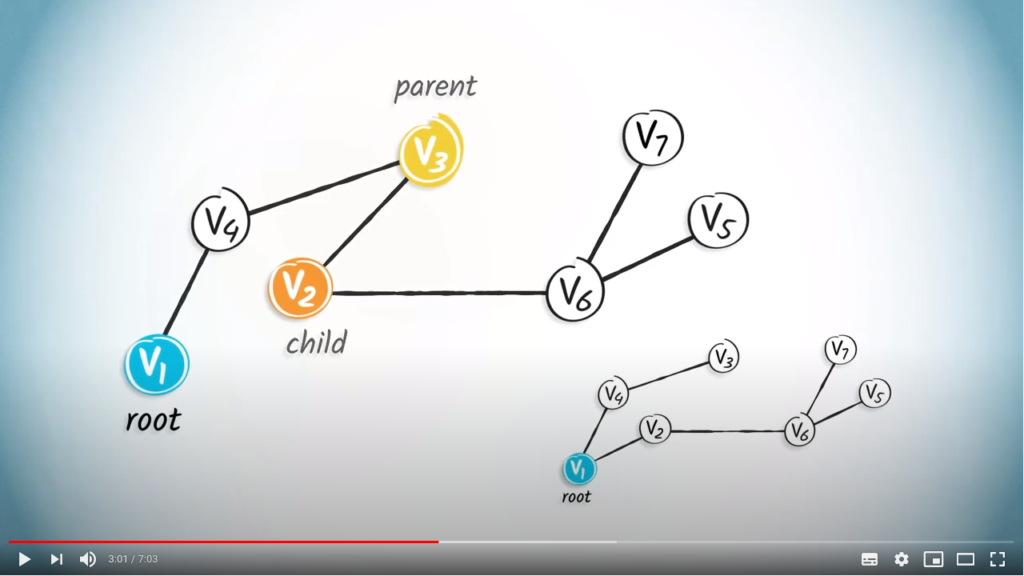
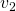 is
is 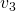 in the tree on the left. Every vertex except the root has a single parent. A child of a vertex
in the tree on the left. Every vertex except the root has a single parent. A child of a vertex  is a vertex of which
is a vertex of which  is the parent. So,
is the parent. So, 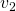 is the child of
is the child of 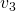 in the tree on the left.
in the tree on the left.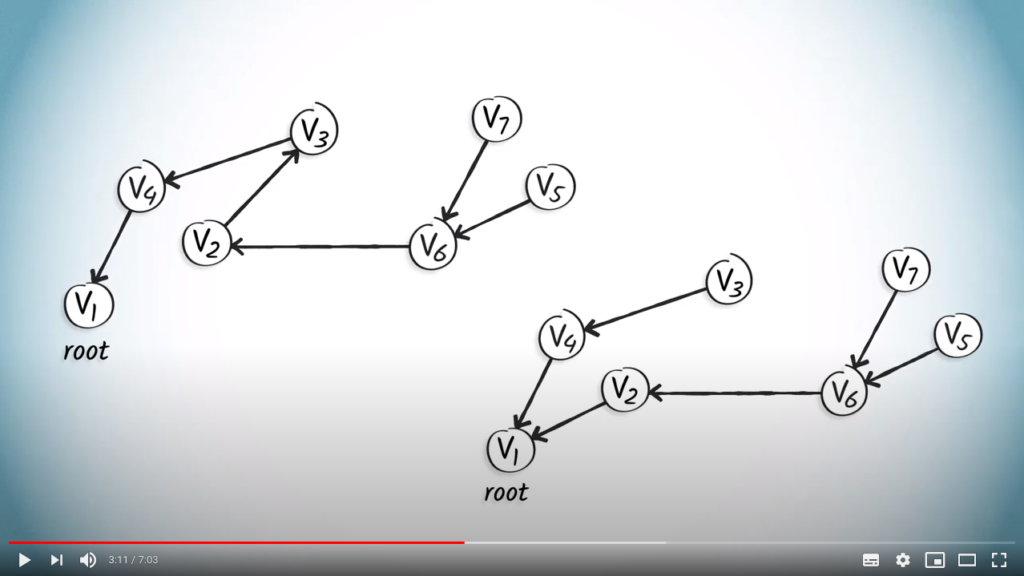
 has no parent, the parent of
has no parent, the parent of  is
is  , and the children of
, and the children of 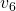 are
are 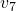 and
and 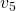 .
.Routing tables
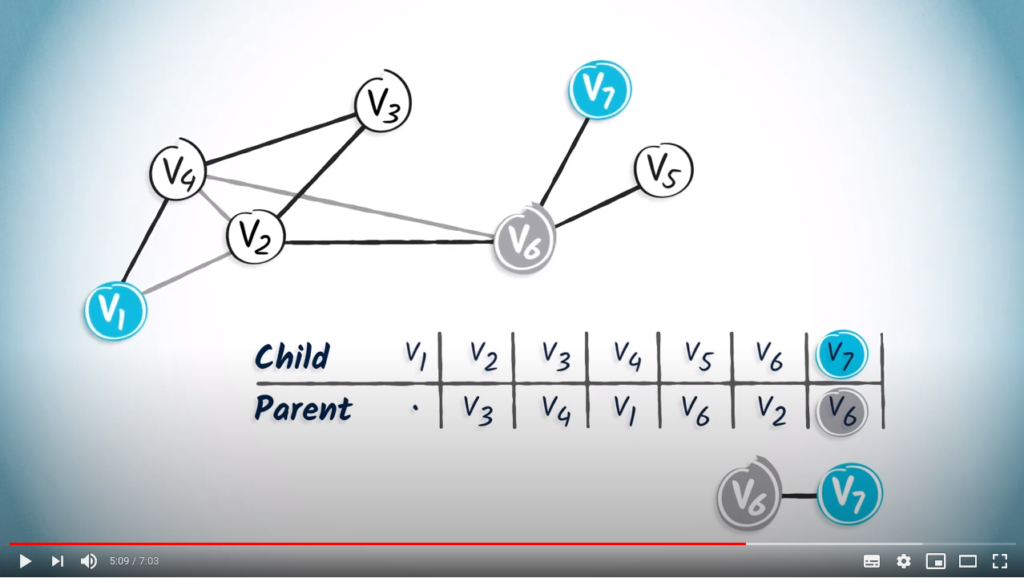
We can now build routing tables by considering the parent of each vertex in the path from ![]() . Routing tables are useful data structures that can be used to reconstruct a path. As we mentioned earlier, routing is considered backwards, from the destination back to the starting position.
. Routing tables are useful data structures that can be used to reconstruct a path. As we mentioned earlier, routing is considered backwards, from the destination back to the starting position.

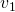 .
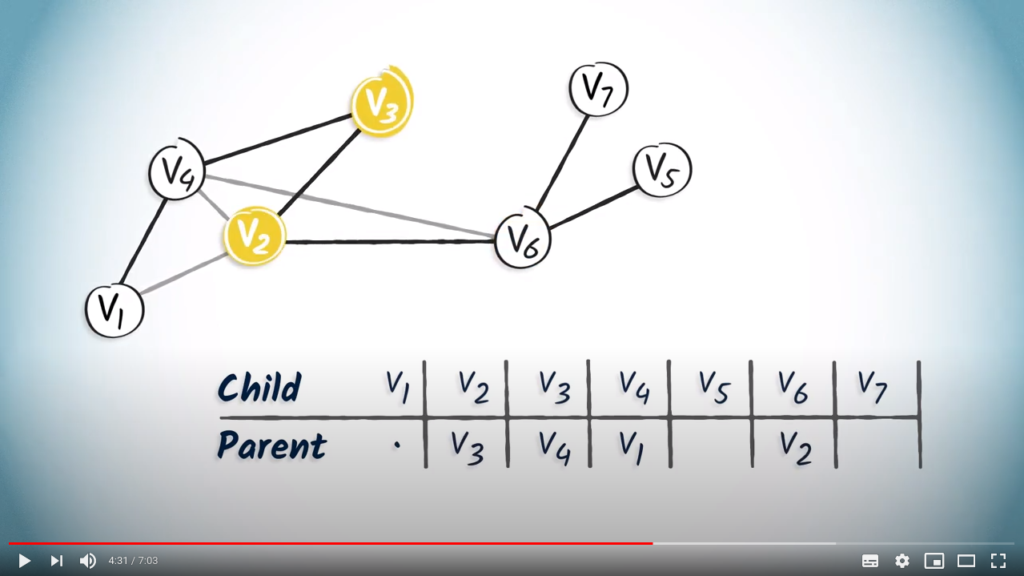
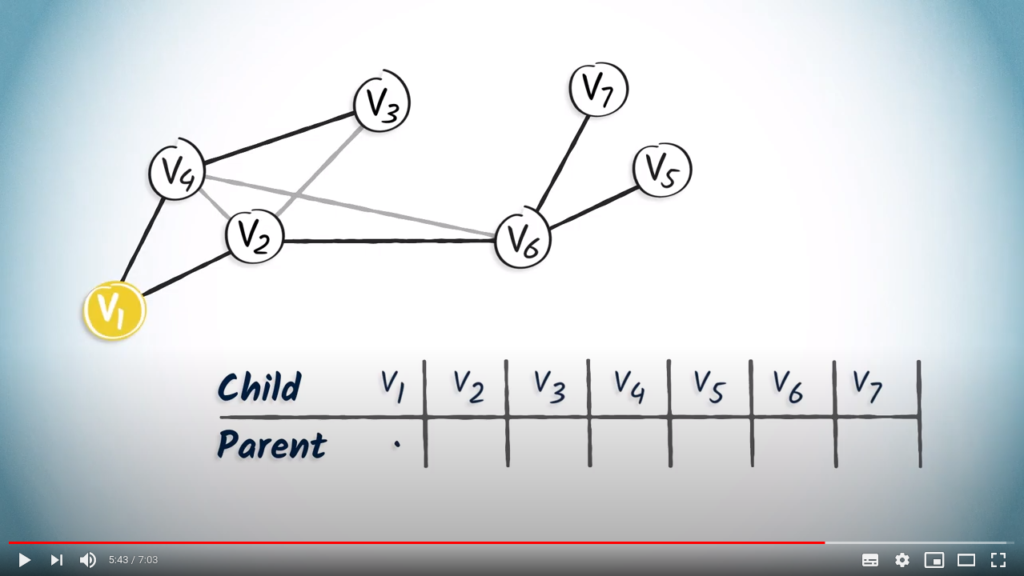
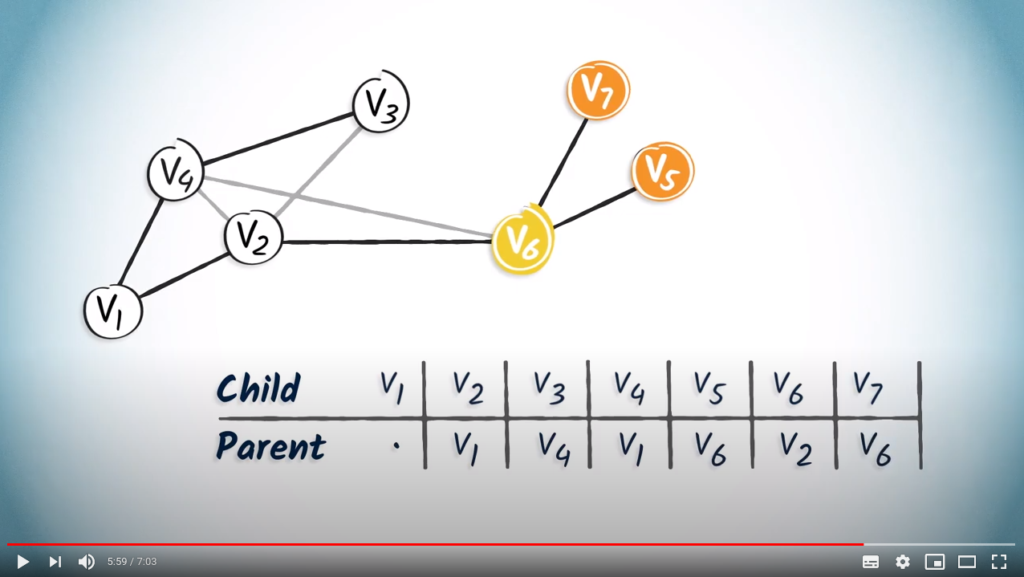
.Let us now see how this table is built step by step using a spanning tree.
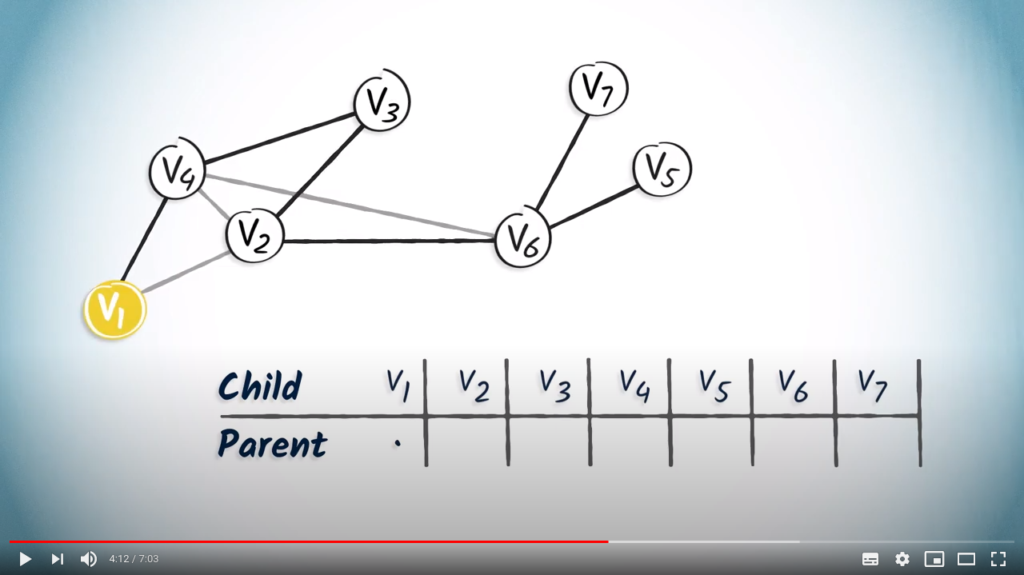
 is the root, so it doesn’t have a parent. We simply note a dot in the
is the root, so it doesn’t have a parent. We simply note a dot in the 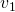 column.
column.
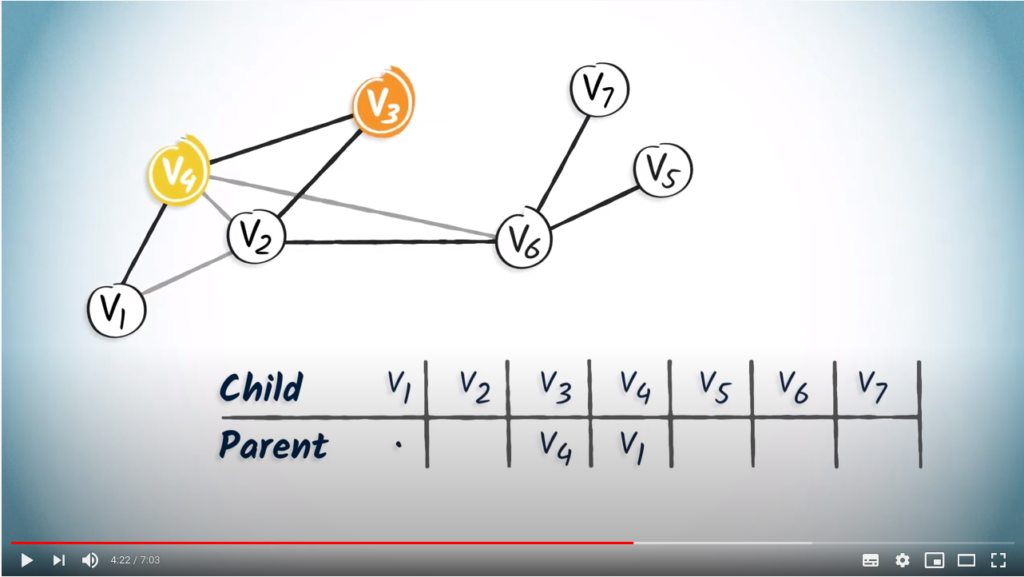
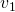 only has one child vertex,
only has one child vertex, 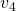 . So we add
. So we add 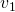 in the column corresponding to
in the column corresponding to 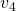 .
.
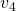 only has one child,
only has one child, 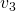 , so we add
, so we add  in the column of
in the column of 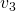 .
.
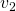 and
and 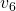 , which are the only children of
, which are the only children of 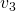 and
and 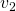 , respectively.
, respectively.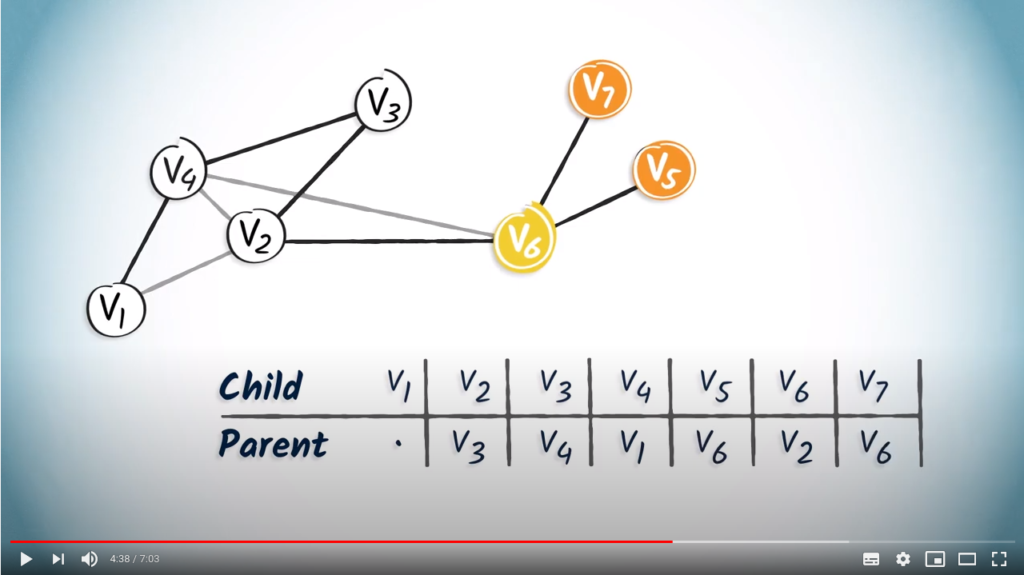
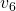 has two children,
has two children, 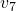 and
and 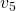 . So, let’s add
. So, let’s add 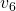 in the columns corresponding to
in the columns corresponding to 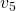 and
and 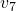 . So that’s it, the routing table is complete.
. So that’s it, the routing table is complete.To read this table, you can simply start from the desired destination and read the corresponding entry, which refers to the parent vertex of the destination.
 to
to 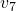 , we first read the entry corresponding to
, we first read the entry corresponding to 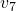 , which is
, which is 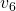 . By definition, the parent of the destination in turn corresponds to the previous vertex in the path from
. By definition, the parent of the destination in turn corresponds to the previous vertex in the path from 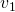 to the destination vertex.
to the destination vertex.
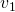 . So in our example, the next step is to identify the entry corresponding to
. So in our example, the next step is to identify the entry corresponding to 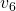 , which is
, which is 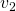 . By continuing like this, we obtain the path
. By continuing like this, we obtain the path 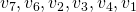 .
.As a second example, let’s also build the routing table from the spanning tree obtained from a BFS.
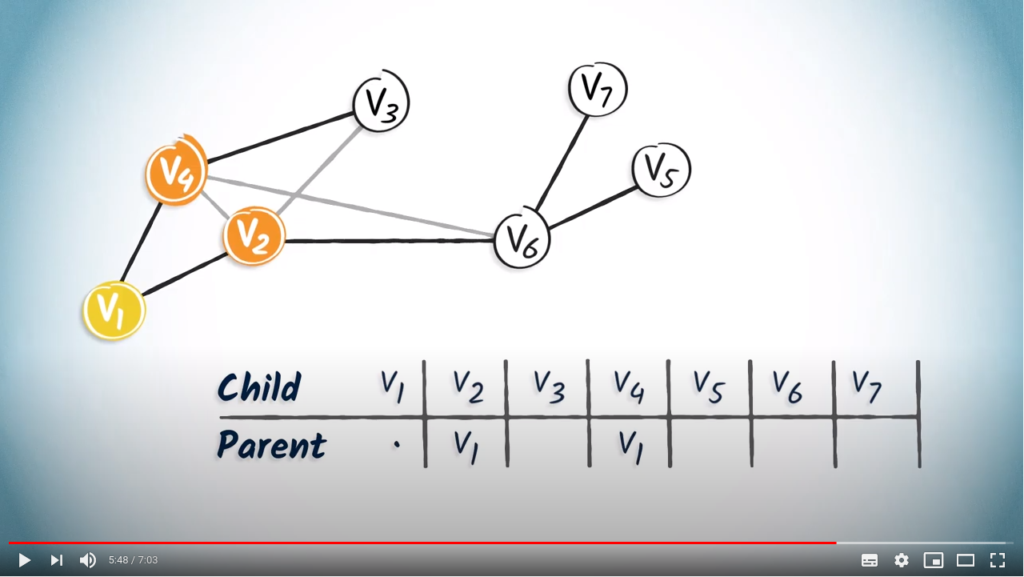
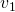 has two children vertices,
has two children vertices, 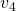 and
and 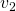 , so we add
, so we add 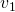 in the corresponding columns.
in the corresponding columns.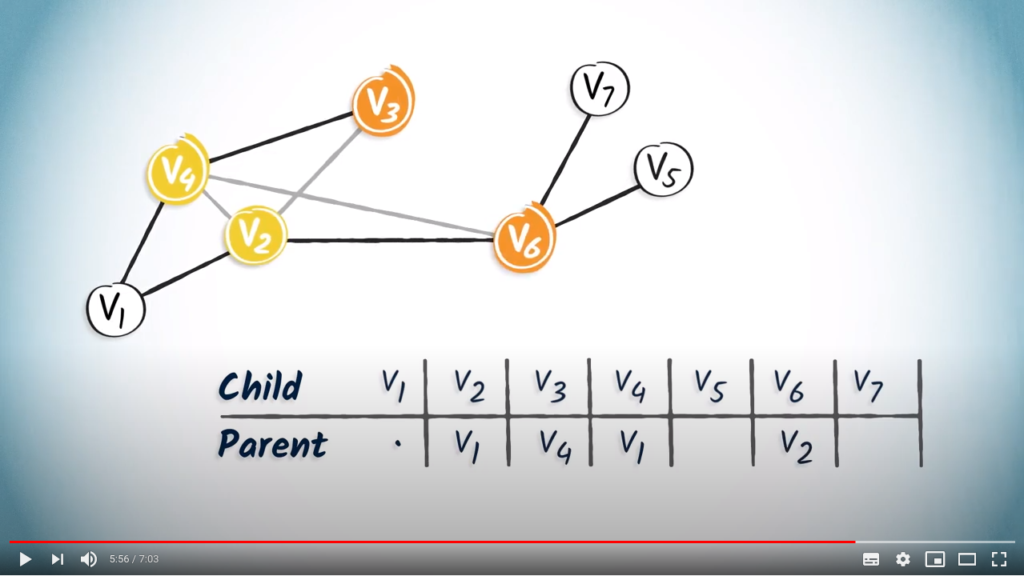
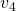 is
is 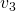 , and the only child of
, and the only child of 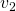 is
is 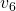 .
.
 has two children,
has two children, 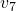 and
and 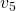 . The routing table is complete.
. The routing table is complete.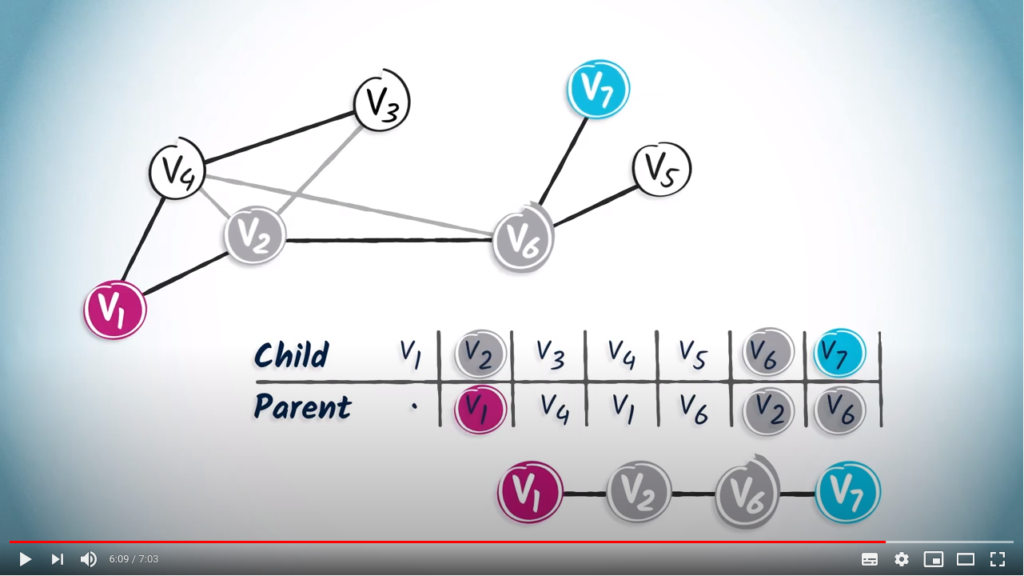
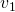 to
to 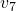 in the table we obtain
in the table we obtain 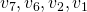 .
.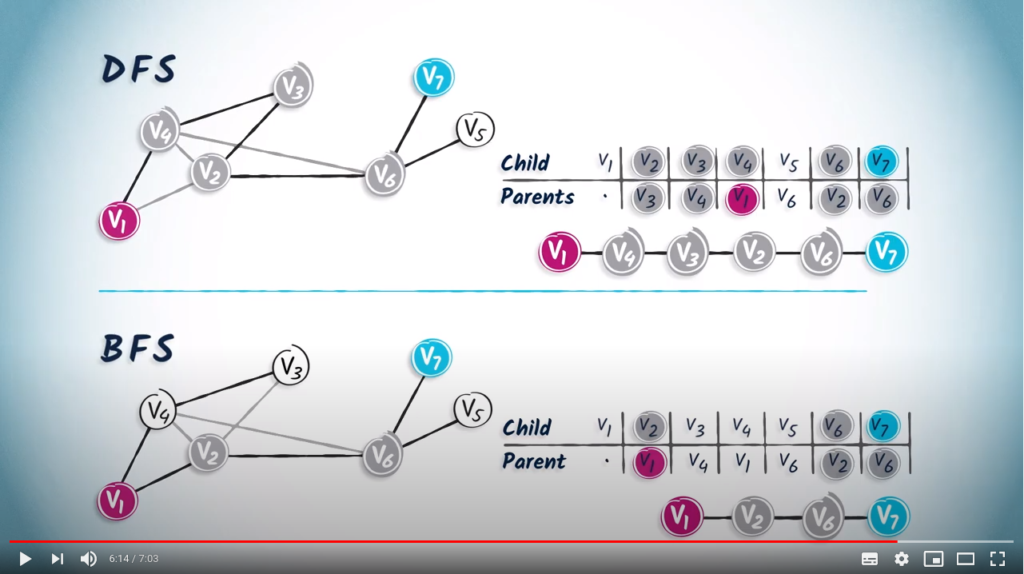
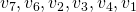 . This is an important difference between DFS and BFS. BFS is a more cautious approach than DFS, as BFS gradually increases the distance from the starting position.
. This is an important difference between DFS and BFS. BFS is a more cautious approach than DFS, as BFS gradually increases the distance from the starting position.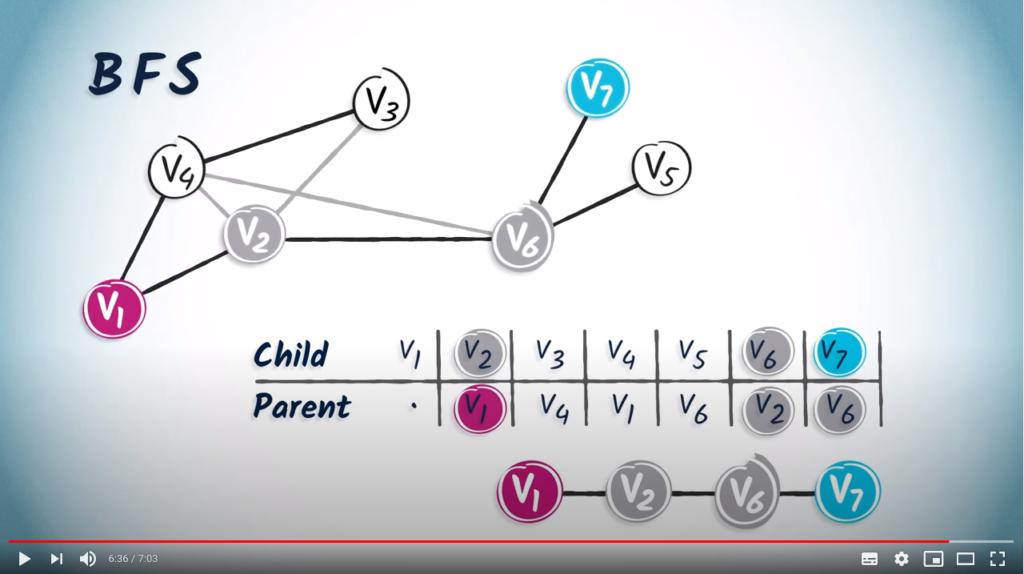
Concluding words
That’s it for today. Thank you for your attention! I’ve really enjoyed talking about routing with you.
You should remember that it is not sufficient to build the spanning tree to navigate between vertices in the graph, but that you also need a routing algorithm.
See you soon for more algorithmic adventures!
Quiz

Time is Up!
