Remark #1: In this video, we have used the terms key (the thing we want to store) and value (its importance in the heap). Other terminologies exist! The only important aspect is that items in the min-heaps should be sorted according to elements of an ordered set.
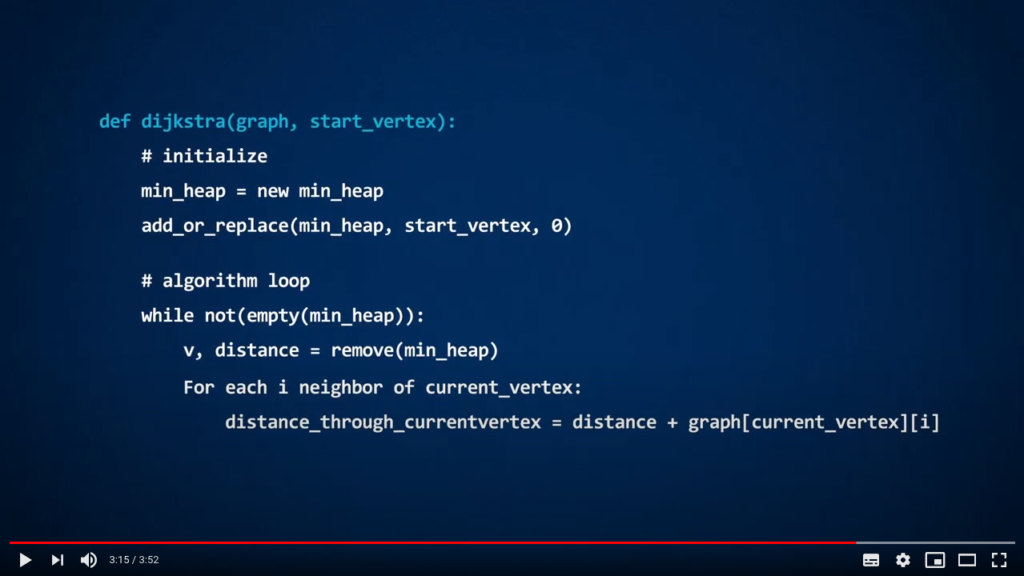
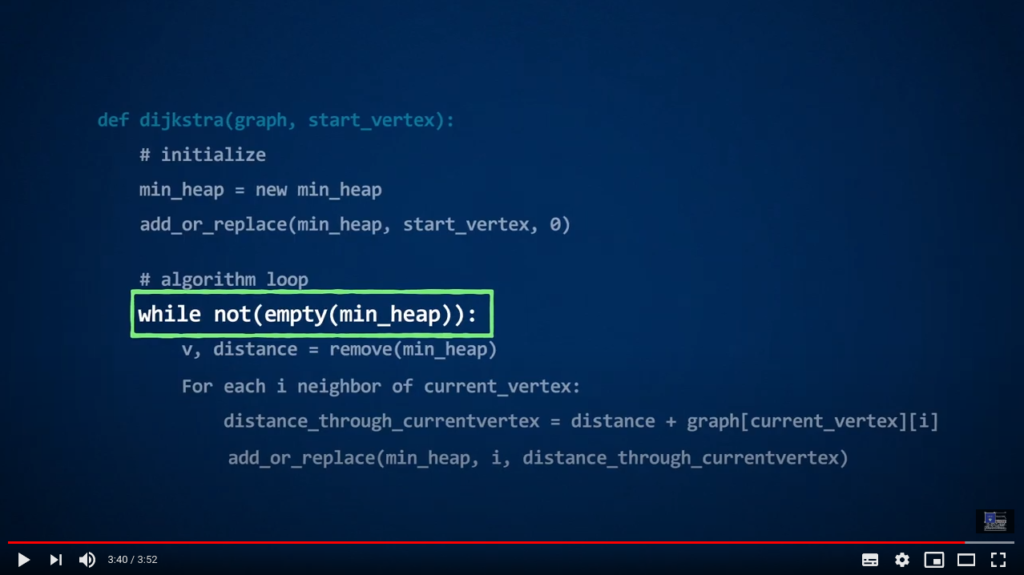
Remark #2: In the video, you are presented a possible implementation of Dijkstra’s algorithm, that uses a function called add_or_replace. Here, we just explain you what the function does but do not provide its code. When implementing the algorithm in Python, you will need to create such a function, or to think otherwise… Indeed, a naive implementation of add_or_replace may have a large complexity, which would impact code performance and energy consumption. On the other hand, we could notice that it is not really a problem if an element has multiple occurrences in the structure, if we can determine which one has the smallest associated value. You will learn more about that in the Lab.
Naive implementation of a priority queue using a list
A simple (yet quite inefficient) way to implement a priority queue is to use a list. This list stores pairs (key, value). Here, we show here how to create a min-heap using a list.
Creation
To create a priority queue using a list, simply create an empty list:
def priority_queue () :
return []
Vacuity test
To test if a priority queue is empty, simply compare it with the empty list:
def is_empty (queue) :
return queue == priority_queue()
Insertion
For insertion and recovery, a choice is available to us. We can either do the expensive work at the time of insertion, for example by maintaining our list sorted in ascending order of values:
def insert (queue, key, value) :
for i in range(len(queue)) :
key_i, value_i = queue[i]
if value < value_i :
return queue[:i] + [(key, value)] + queue[i:]
return queue + [(key, value)]
Or do so at the time of recovery, looking for the smallest value. So we simply add the item to the list:
def insert (queue, key, value) :
return queue + [(key, value)]
Extraction
To retrieve the element with the smallest value in this priority queue (and the remaining priority queue), we find ourselves with two versions, depending on the scenario chosen for insertion. For version 1:
def extract (queue) :
return queue[0], queue[1:]
For version 2:
def extract (queue) :
min_i = 0
min_key, min_value = queue[min_i]
for i in range(len(queue)) :
key, value = queue[i]
if value < min_value :
min_key = key_i
min_value = value_i
min_i = i
return (min_key, min_value), queue[:min_i] + queue[min_i+1:]
Tests
To test our functions, let’s execute the following commands:
# Structure preparation
queue = priority_queue()
queue = insert(queue, "five", 5)
queue = insert(queue, "three", 3)
queue = insert(queue, "eight", 8)
# [('three', 3), ('five', 5), ('eight', 8)] if solution 1 is chosen
# [('five', 5), ('three', 3), ('eight', 8)] if solution 2 is chosen
print(queue)
# "three", then "five", then "eight"
while not empty(queue) :
(key, value), queue = extract(queue)
print(value)
# []
print(queue)
Complexity
The problem with this implementation is the complexity of the operations. Depending on the version, either insertion or recovery requires browsing the entire list, leading to a number of elementary operations at least proportional to the size of the list (i.e., ![]() , with
, with ![]() the number of items in the list). In practice this complexity is far too great.
the number of items in the list). In practice this complexity is far too great.
Implementation using a balanced binary tree
Definitions
Let us start with a few definitions. You should already know what a tree is, and what we call its root.
A vertex in a tree is a node if it has neighbors farther from the tree root (which we call children). If not, it is a leaf.
The depth of a tree is the length of the longest shortest path starting from the root.
A tree is balanced if all its shortest paths starting from the root have the same length, ![]() .
.
The tree model we will use
Instead of using a list, it is proposed to use a balanced binary tree with the following properties:
- Each node of the tree is associated with a couple (key, value). This property makes it possible to link the tree to the elements to be stored/extracted.
- Every parent node has two children, unless the total number of elements in the priority queue is even, in which case a single node has only one child and all the others have two.
Note: Ternary/quaternary/quaternary/etc. trees could also have been considered (this changes the number of children). As the number of children increases, the complexity of the insertion operation decreases, but the complexity of the extraction increases. - The tree is balanced. This property ensures that the tree does not have a shape similar to a long chain, by making a kind of list, thus losing all the interest of using trees.
- A parent’s value is always smaller than that of his sons. This essential property ensures that the minimum value node is always at the root.
Creation
To initialize such a priority queue, simply return an empty tree.
Vacuity test
To test if a priority queue is empty, check if it is equal to an empty tree.
Insertion
To insert a couple (key, value) into the tree, proceed as follows:
- The couple (key, value) is added at the end of the tree, i.e.:
- If all parent nodes have two children, a leaf of minimum depth is transformed into a parent of this node.
- If a parent node has only one child, it is added as a second child this node.
- If the value of this new node is smaller than that of its parent, the couples (key, value) of the node and its parent are exchanged.
- We continue by going back up the tree as much as necessary.
Since we are only replacing elements in the tree with ones of smaller values, the resulting tree keeps the stated properties if the original one had them.
Extraction
To retrieve an element, proceed as follows:
- The couple (key, value) associated with the root of the tree is returned.
- We replace it with one leaf of maximum depth of the tree.
- If the new root has a value larger than one of its children, the couple (key, value) is exchanged with the child with smallest value.
- We start again by going down as much as necessary.
Here again, it is easy to check that the resulting tree respects the stated properties if the starting tree also respects them.
Complexity
The complexity of insertion and extraction operations requires to go from the root to a leaf of maximum depth in the worst case. The tree being binary, this represents ![]() operations, where
operations, where ![]() is the number of elements in the queue. We are therefore much less complex than with a naive implementation using a list (where the number of operations was at least linear in
is the number of elements in the queue. We are therefore much less complex than with a naive implementation using a list (where the number of operations was at least linear in ![]() ).
).
To go further
- A more complete list of priority structures.
- Priority structures help developing heuristics for visiting neighbors.
- Python’s heapq module: in practice, you should use this for PyRat.



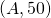 ,
, 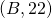 and
and 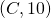 .
.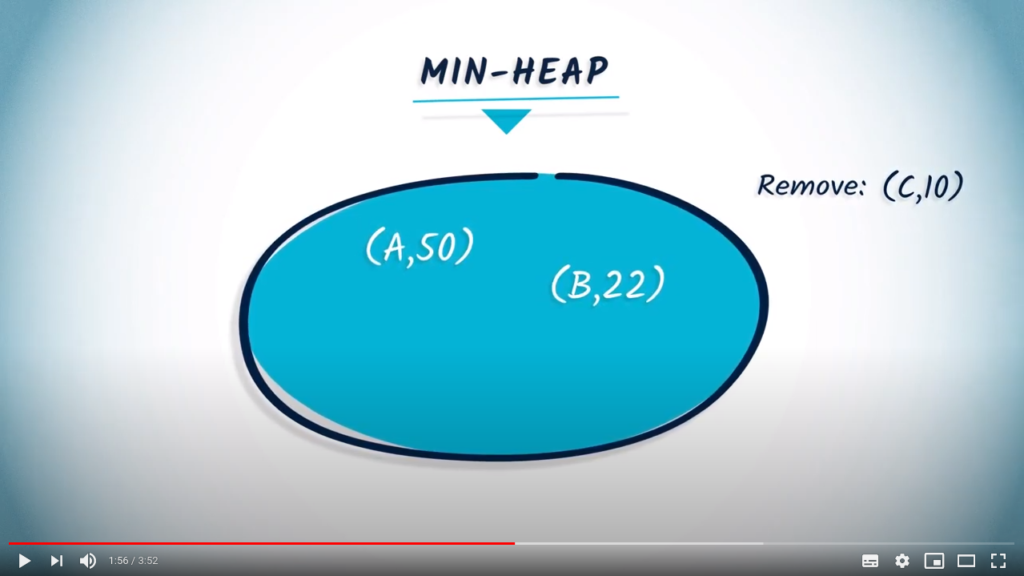
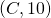 , and the status of the min-heap will be
, and the status of the min-heap will be 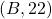 .
.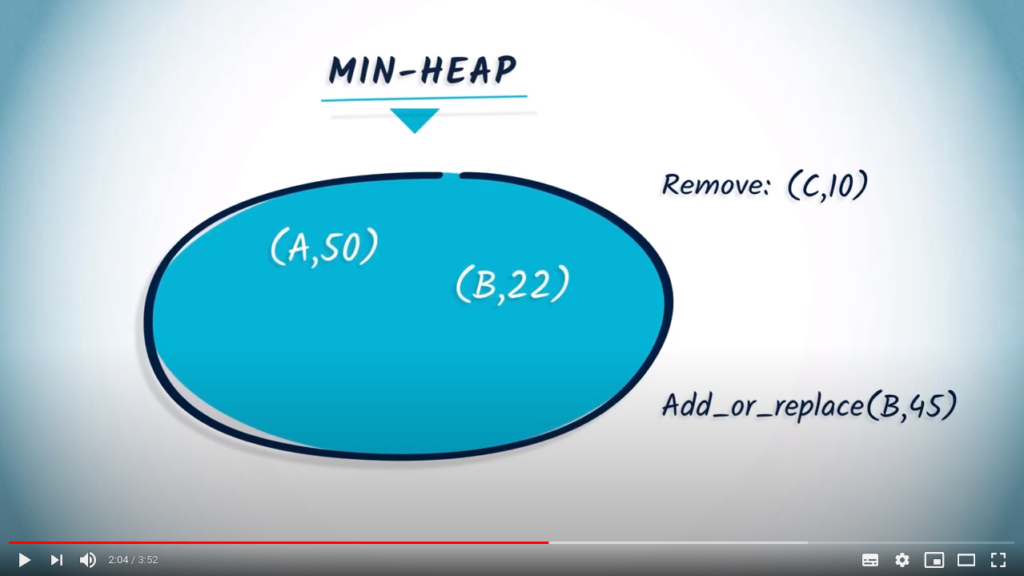
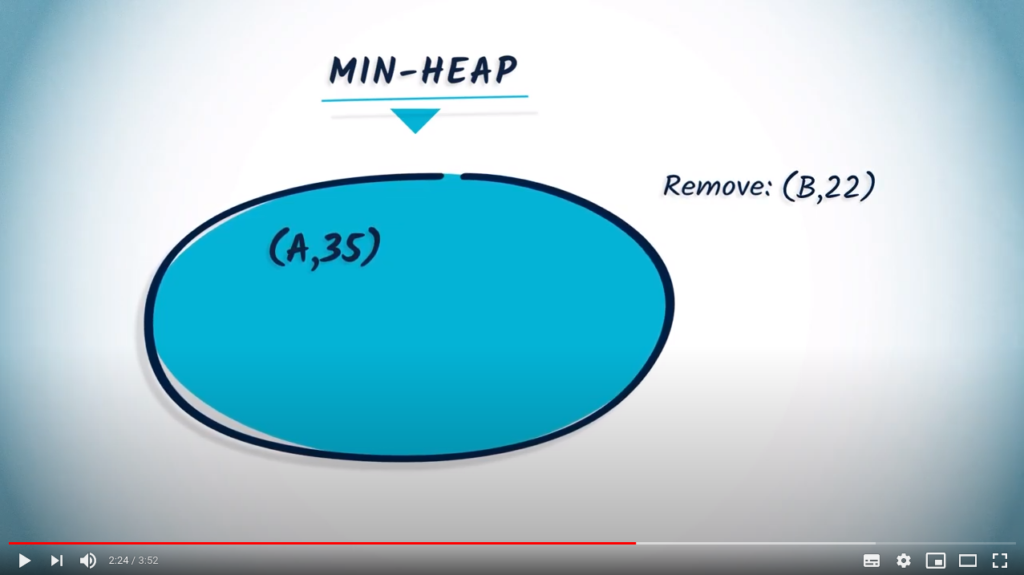
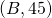 . Because 45 is larger than 22, nothing happens.
. Because 45 is larger than 22, nothing happens.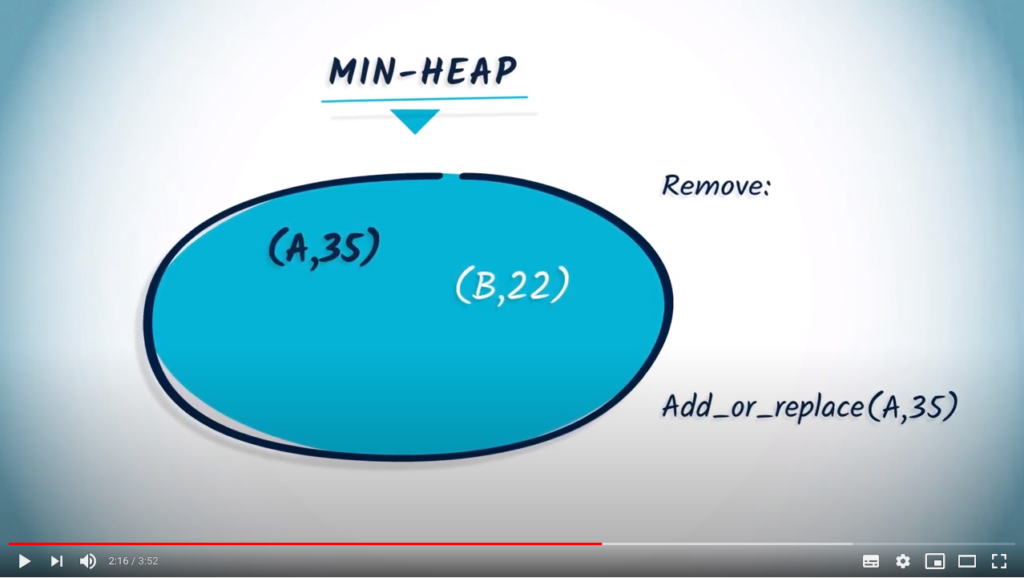
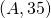 . 35 is smaller than 50, and so the entry corresponding to
. 35 is smaller than 50, and so the entry corresponding to  will be updated, resulting in the following min-heap.
will be updated, resulting in the following min-heap.